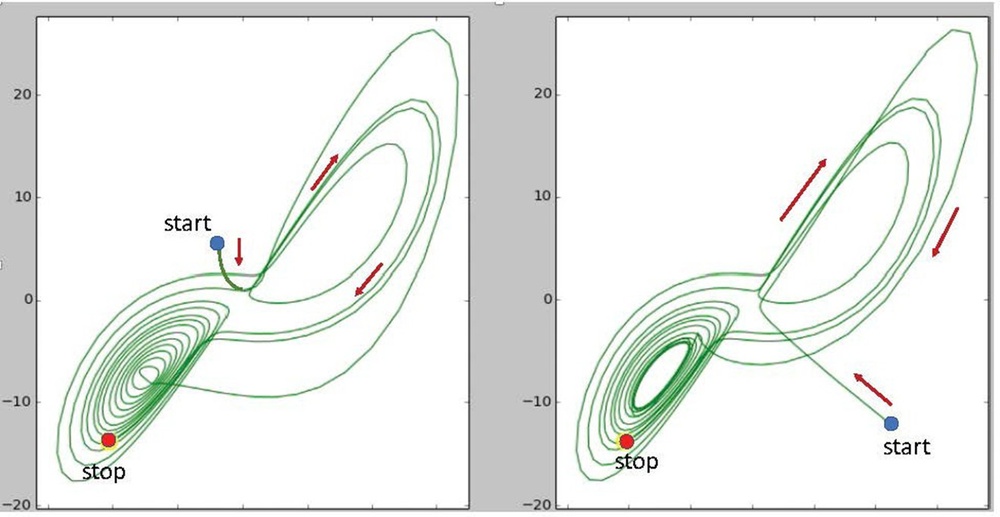
The figure shows two chaotic systems starting in very different places in their orbits, but soon synchronize and do a "dance" much like synchronized swimmers. Despite the complicated orbits, they come to follow each other almost exactly. Stopping after a short time shows they are both in the same state. This will never happen with two chaotic systems, which unconnected will have motions completely uncorrelated with each other. Note the systems can be remotely located from each other and signals connecting them the right way will cause synchronization. (Figure provided by U.S. Naval Research Laboratory)
| Date Taken: | 10.06.2020 |
| Date Posted: | 10.06.2020 10:51 |
| Photo ID: | 6381457 |
| VIRIN: | 201006-N-NO204-002 |
| Resolution: | 1319x682 |
| Size: | 153.19 KB |
| Location: | US |
| Web Views: | 12 |
| Downloads: | 2 |

This work, Chaotic Systems, by Daniel Parry, identified by DVIDS, must comply with the restrictions shown on https://www.dvidshub.net/about/copyright.